ReLU Function คืออะไร ทำไมถึงนิยมใช้ใน Deep Neural Network ต่างกับ Sigmoid อย่างไร – Activation Function ep.3

เรามาถึง Activation Function ep.3 เรื่อง ReLU Function ซึ่งเป็นฟังก์ชันที่นิยมใช้ในการเทรน Deep Learning มากที่สุดในปัจจุบัน เมื่อเราดูโครงสร้างภายในโมเดล Deep Neural Network ชื่อดังสมัยใหม่ ก็จะเห็นแต่ ReLU เต็มไปหมด แล้ว ReLU มีดีตรงไหน ต่างกับ Sigmoid และ Tanh อย่างไร เราจะมาเรียนรู้กัน

ReLU Function

ReLU ย่อมาจาก Rectified Linear Unit คือ ฟังก์ชันเส้นตรงที่ถูกปรับแก้ Rectified ไม่ได้เป็นรูปตัว S เหมือน 2 ฟังก์ชันก่อนหน้า ReLU เป็นฟังก์ชันที่เรียบง่ายกว่าทุก Activation Function ที่ผ่านมา แต่ทรงพลัง เนื่องจาก ถ้า Input เป็นบวก Slope จะเท่ากับ 1 ตลอดกาล ทำให้ Gradient ไม่หาย (ไม่เกิด Vanishing Gradient) ส่งผลให้เราเทรนโมเดลได้เร็วขึ้นมาก

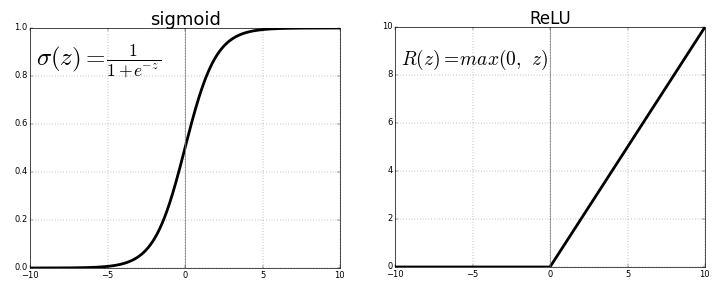
สมการของ ReLU Function

\(f(x) = \max(0, x) = \begin{cases}
0 & \text{for } x \le 0\\
x & \text{for } x > 0\end{cases}\)

Derivative ของ ReLU Function

ถ้า x เป็นบวก Derivative ของ ReLU Function = 1 กุญแจสำคัญที่ช่วยให้การเทรน Deep Neural Network ทำได้รวดเร็วมากขึ้น

\(f'(x) = \begin{cases}
0 & \text{for } x \le 0\\
1 & \text{for } x > 0\end{cases}\)

แต่ตอนนี้เรายังไม่ต้องสนใจ สมการสูตรคณิตศาสตร์ เรามาดูกันว่า ReLU Function จริง ๆ แล้ว Input/Output ของมันมีหน้าตาเป็นอย่างไร เปรียบเทียบกับ Sigmoid Function

เรามาเริ่มกันเลย

ข้อดีของ ReLU Function

1. Slope เป็น 1 ทำให้ Gradient ไม่หาย ลดปัญหา Vanishing Gradient ช่วยให้เราเทรนโมเดลได้อย่างรวดเร็ว
2. หา Derivative ไม่ยาก Derivative เป็น 0 ไม่ก็ 1 ขึ้นกับ Input
3. ใช้แล้วโมเดล Converge เร็วขึ้นมาก

ข้อเสียของ ReLU Function

1. Output ไม่ Balance มี Mean ไม่เท่ากับ 0 เพราะมีแต่ค่าเป็นบวก ทำให้ Optimize ยาก
2. Output อยู่ในช่วง 0-Infinity ไม่มี Limit จัดการลำบาก
3. ถ้า Input เป็นค่าติดลบ Output จะเป็น 0 เสมอ ทำให้ยากต่อการแปลงค่ากลับ

แต่ข้อดีที่ Gradient ไม่หาย ลดปัญหา Vanishing Gradient ทำให้เราเทรนโมเดลได้รวดเร็ว ชนะทุกสิ่ง ทำให้เรามองข้ามข้อเสียของมันไป (ข้อเสียเหล่านี้ยังพอจัดการได้ แต่ Gradient หายแก้ไม่ได้)

เรื่อง Gradient จะอธิบายต่อไป ในหัวข้อ Optimization

มีผู้ออกแบบ Leaky ReLU เพื่อมาแก้ไขข้อเสียของ ReLU โดยแทนที่ Output จะเป็น 0 เสมอ ถ้า Input ติดลบ ก็ให้เป็นค่าติดลบน้อย ๆ แทน จะได้ยังสามารถแปลงค่ากลับได้ แต่ก็ยังไม่ค่อยได้รับความนิยมเท่าที่ควร

Train Neural Network

Deep Neural Network with 2 Hidden Layers using ReLU

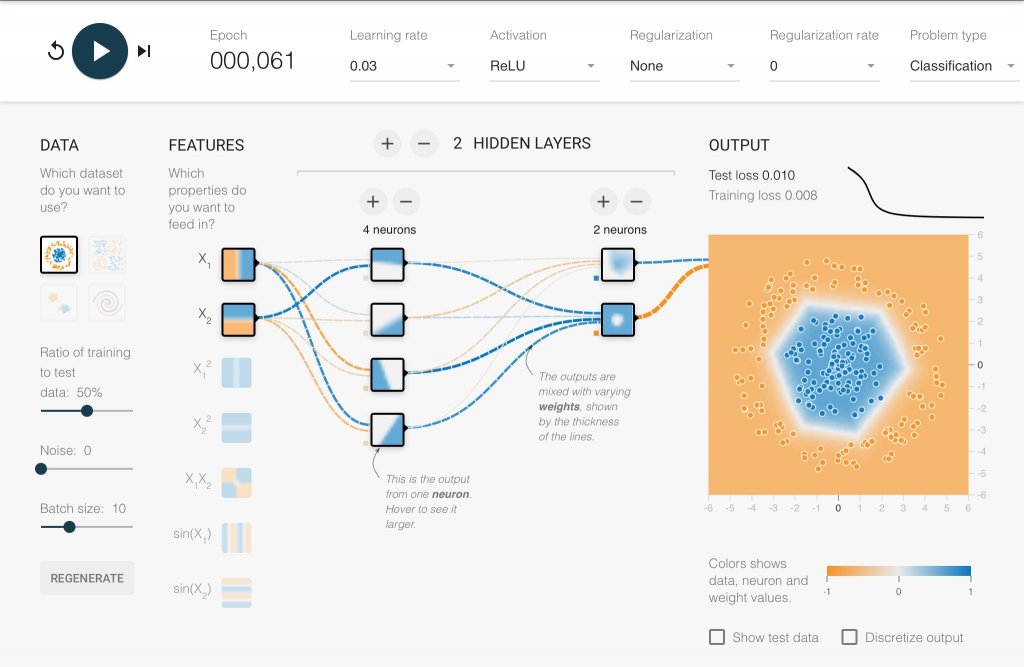
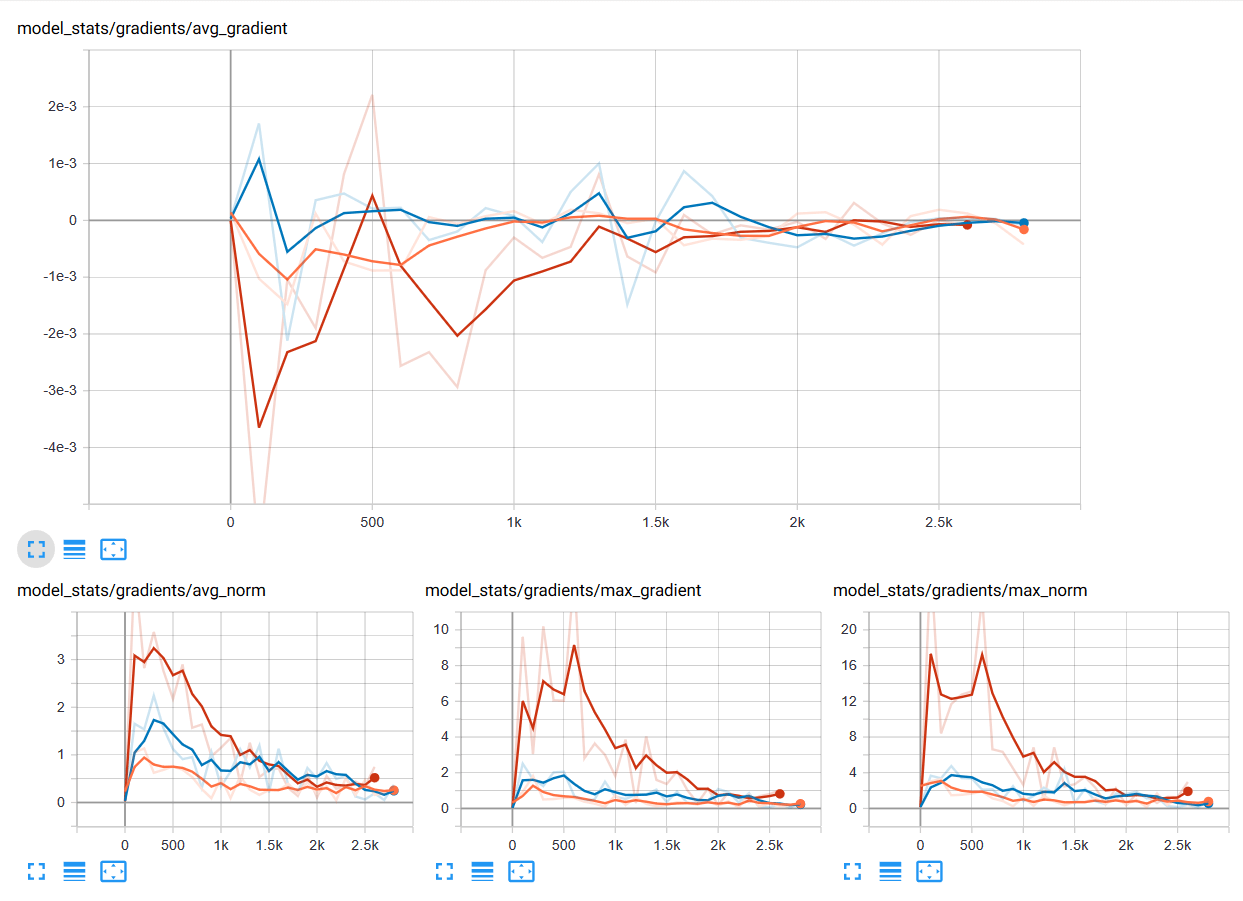
สังเกตว่าเพียง 61 Epoch เท่านั้น ก็ Converge แถมช่วงแรก Training Loss และ Test Loss ลดลงเร็วมาก เปรียบเทียบกับ Tanh 100+ Epoch, Sigmoid 1000+ Epoch

Credit

• http://cs231n.github.io/neural-networks-1/
• https://towardsdatascience.com/activation-functions-neural-networks-1cbd9f8d91d6
• https://en.wikipedia.org/wiki/Rectifier_(neural_networks)
• https://en.wikipedia.org/wiki/Activation_function
• https://playground.tensorflow.org