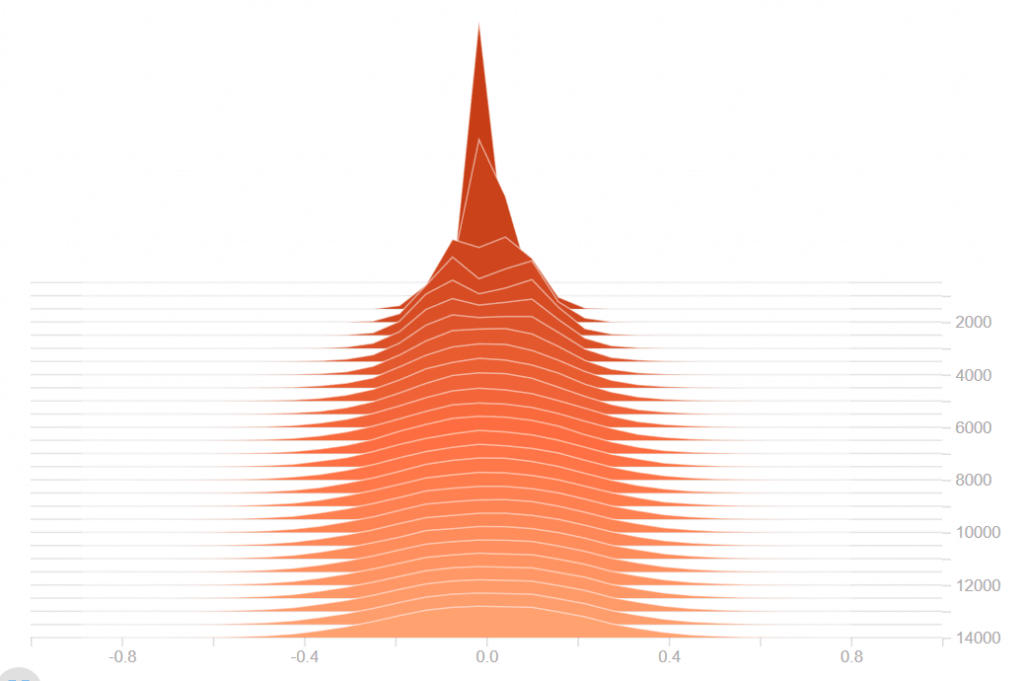
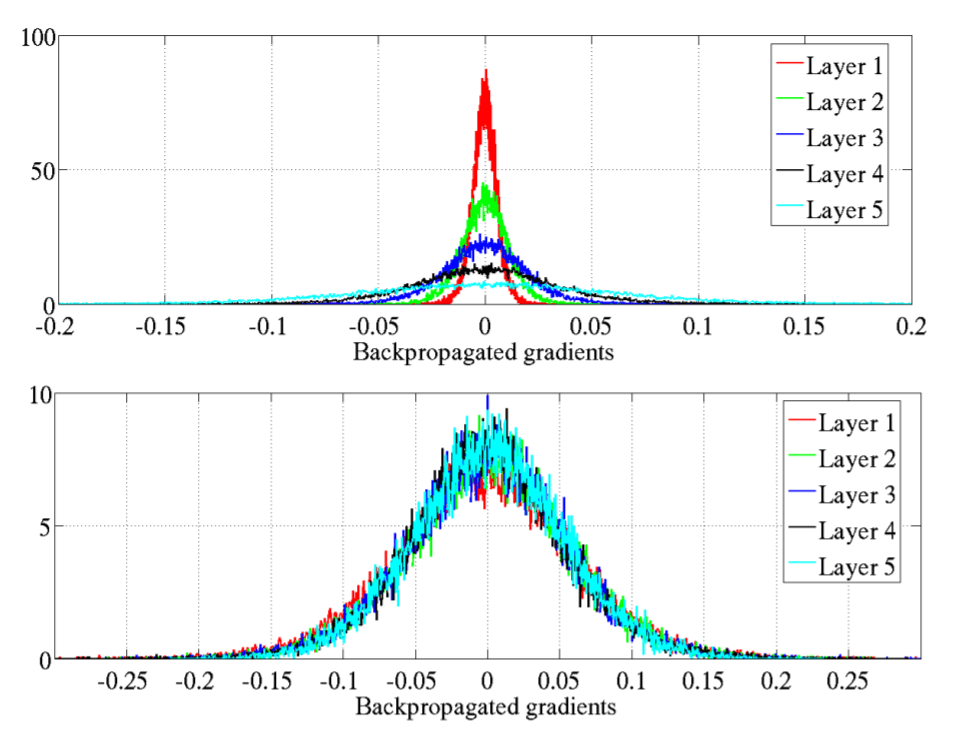
ใน ep ที่แล้วเราได้เรียนรู้ถึงปัญหา Vanishing Gradient Problem และวิธีแก้ไขกันไปแล้ว ใน ep นี้เราจะเจาะลึกลงไปถึงสาเหตุ ดูตัวอย่างของ Neural Network ว่าเมื่อเกิดปัญหา Vanishing Gradient Problem และ Exploding Gradient Problem จะมีอาการอย่างไร และเราจะแก้ไขอย่างไรให้โมเดลสามารถเทรนได้ต่อ

Vanishing Gradient from Tensorboard
Vanishing Gradient from Tensorboard

เรามาเริ่มกันเลยดีกว่า

Open In Colab

แชร์ให้เพื่อน:

Share

บทความที่เกี่ยวข้อง:

  1. Vanishing Gradient Problem คืออะไร แก้ Vanishing Gradient Problem ด้วย Xavier Initialization และ Kaiming Initialization – Neural Network ep.2
  2. Layer-Sequential Unit-Variance Initialization (LSUV) คืออะไร แตกต่างกับ Kaiming อย่างไร ในการ Initialize Deep Neural Network – ConvNet ep.6
  3. BatchNorm คืออะไร สอน Batch Normalization เทรน Machine Learning โมเดล Deep Convolutional Neural Network – ConvNet ep.5
  4. Neural Network คืออะไร Artificial Neural Network ทำงานอย่างไร สอนสร้าง Deep Neural Network แบบเข้าใจง่าย – Neural Network ep.1
Surapong Kanoktipsatharporn on Linkedin
Surapong Kanoktipsatharporn
CTO at Bua Labs
The ultimate test of your knowledge is your capacity to convey it to another.

Published by Surapong Kanoktipsatharporn

The ultimate test of your knowledge is your capacity to convey it to another.