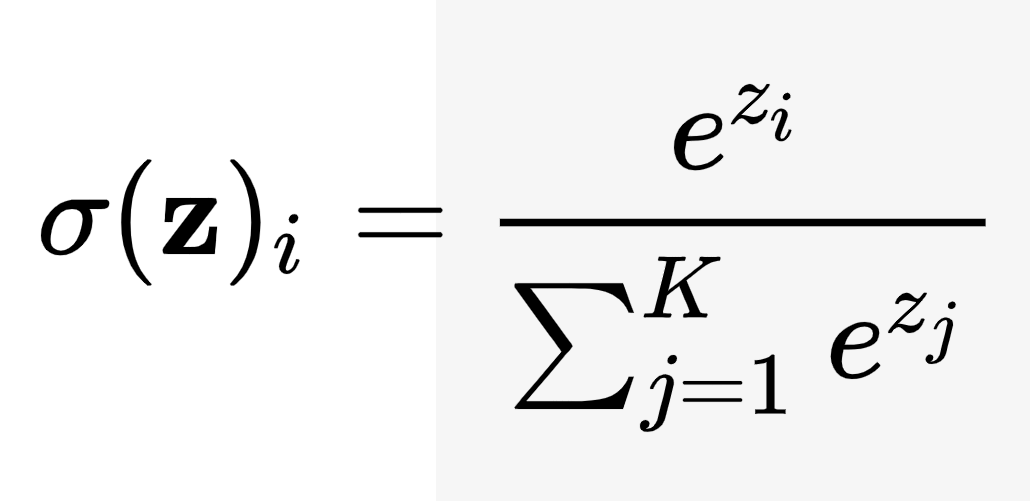Softmax Function คืออะไร เราจะใช้งาน Softmax Function อย่างไร ประโยชน์ของ Softmax

Softmax Function หรือ SoftArgMax Function หรือ Normalized Exponential Function คือ ฟังก์ชันที่รับ Input เป็น Vector ของ Logit จำนวนจริง แล้ว Normalize ออกมาเป็นความน่าจะเป็น Probability ที่ผลรวมเท่ากับ 1

หรือเข้าใจง่าย ๆ ว่า Softmax รับตัวเลขเข้าไป แล้วแปลงออกมาเป็น Probability เรามาดูตัวอย่างกันจะเข้าใจง่ายขึ้น

สูตร Softmax

\(\sigma(\mathbf{z})i = \frac{e^{z_i}}{\sum{j=1}^K e^{z_j}} \text{ for } i = 1, \dotsc , K \text{ and } \mathbf z=(z_1,\dotsc,z_K) \in R^K\)

ประโยชน์ของ Softmax Function

Softmax มักถูกนำไปไว้ Layer สุดท้าย ของ Neural Network เพื่อให้ Output ออกมาเป็น Probability ไปคำนวน Negative Log Likelihood เป็น Cross Entropy Loss เช่น ในงาน Single Class Classification

Softmax ถูกนำไปใช้บ่อย ในงาน Classification จนถึงขนาดมีคนเรียกว่า Softmax Classifier หรือ Softmax Loss

ข้อเสียของ Softmax Function

1. เหมาะกับการใช้งานที่คาดหวัง Output ที่ถูกต้องอันเดียวเท่านั้น (ใกล้เคียง Max Function)
2. เนื่องจาก ตัวหารต้อง Sum รวมทั้งหมดทุก Item ทุกครั้ง จึงทำให้มีปัญหาเรื่อง Performance ถ้ามีจำนวน Item มาก ๆ เช่น Output เป็น 1 ใน 500,000 คำใน Dictionary ในงาน NLP

เรามาเริ่มกันเลย