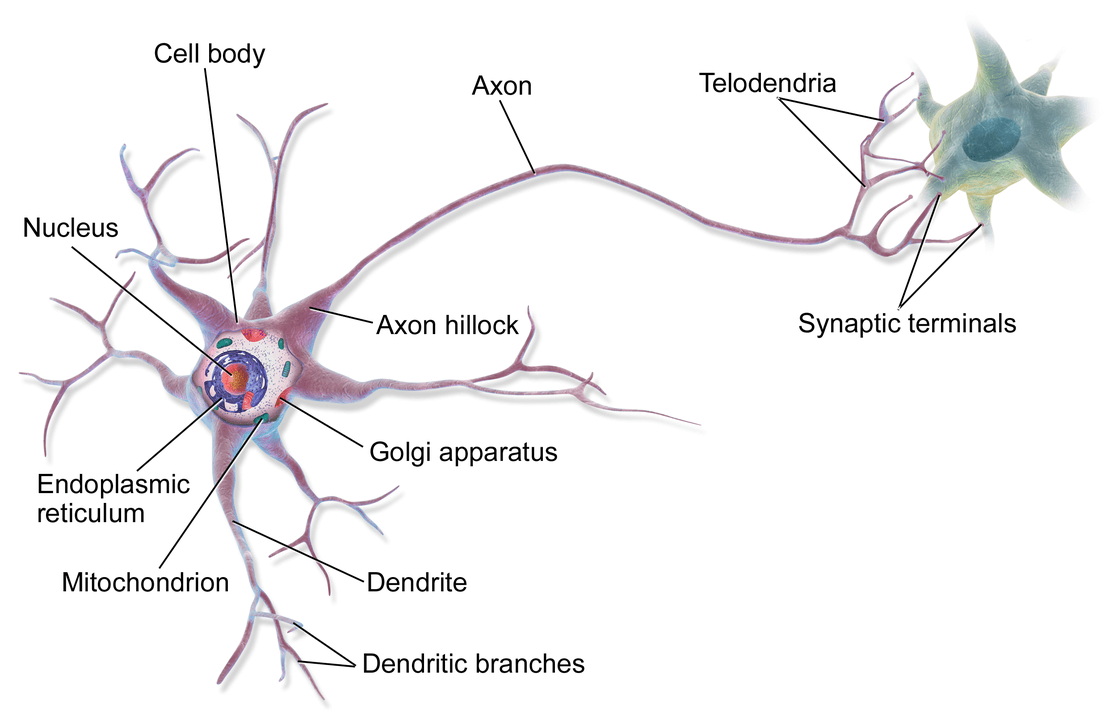
ในสมองของมนุษย์คนหนึ่ง จะประกอบด้วยหน่วยเล็ก ๆ เรียกว่า นิวรอน (Neuron) จำนวนประมาณ 8 หมื่น 6 พันล้านนิวรอน ดังรูปด้านบน และแต่ละนิวรอนก็จะเชื่อมต่อโยงใยกันด้วยเส้นประสาทเรียกว่า ไซแนปส์ (Synapse) รวมแล้วประมาณ 1 พันล้านล้านไซแนปส์ ซึ่งนักวิทยาศาสตร์คอมพิวเตอร์ได้นำมาเป็นแนวคิดในการออกแบบ Artificial Neural Network
แต่ละนิวรอน จะได้รับ Input หลาย ๆ อันจากหลาย ๆ กิ่งก้านสาขาของ Dendrite แล้วนำมาประมวลผล ออกมาเป็น Output 1 อัน ออกไปที่ Axon เพื่อส่งต่อไปให้ Dendrite ของนิวรอนอื่น ๆ ใช้เป็น Input ต่อไป เราสามารถเขียนเป็นโมเดลได้ดังด้านล่าง
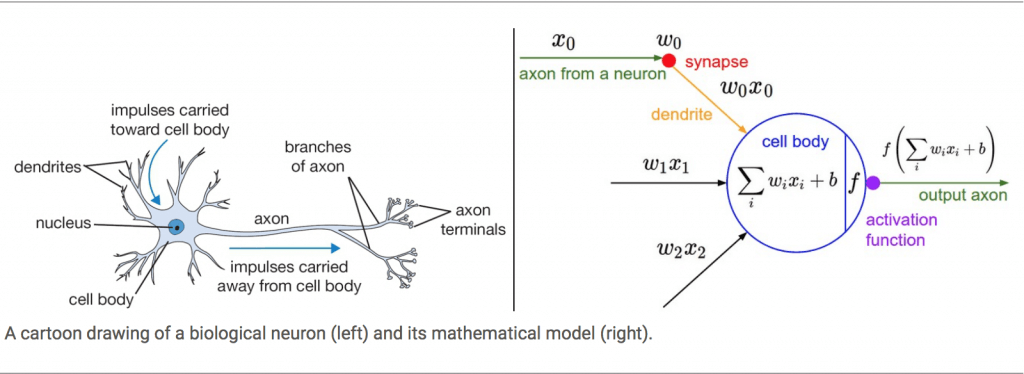
Activation Function
Activation Function คือ ฟังก์ชันที่รับผลรวมการประมวลผลทั้งหมด จากทุก Input (ทุก Dendrite) ภายใน 1 นิวรอน แล้วพิจารณาว่าจะส่งต่อเป็น Output เท่าไร (เปรียบเทียบกับความถี่ของสัญญาณประสาท Output ใน Axon)
เรื่องระบบการทำงานภายใน Artificial Neural Network จะอธิบายต่อไป
Activation Function ที่เป็นที่นิยมในอดีต คือ Sigmoid Function ที่รับข้อมูลอะไรก็ตามเข้าไป เปลี่ยนเป็นค่าระหว่าง 0-1
Sigmoid Function
Sigmoid Function เป็นฟังก์ชันที่เป็น Curve รูปตัว S เห็นแล้วเข้าใจได้ง่าย และเนื่องจาก Output ของ Sigmoid Function มีค่าระหว่าง 0 – 1 จึงเหมาะที่จะถูกใช้ในงานที่ต้องการ Output เป็นความน่าจะเป็น (Probability) หรือใช้เป็น Output ว่า 1=Yes, 0=No
สมการของ Sigmoid Function
\(S(x) = \frac{1}{1 + e^{-x}} = \frac{e^x}{e^x + 1}\)Derivative ของ Sigmoid Function
Derivative ของ Sigmoid Function ก็สามารถคำนวนได้ง่าย ๆ จากค่าของ Sigmoid Function เอง ดังนี้
\(S'(x) = S(x)(1 – S(x))\)แต่ตอนนี้เรายังไม่ต้องสนใจ สมการสูตรคณิตศาสตร์ เรามาดูกันว่า Sigmoid Function จริง ๆ แล้ว Input/Output ของมันมีหน้าตาเป็นอย่างไร
เรามาเริ่มกันเลยดีกว่า
ข้อดีของ Sigmoid Function
- Output อยู่ในช่วง 0-1 ใช้งานได้หลากหลาย ทั้ง Probability, Boolean
- เข้าใจง่าย
- หา Derivative ไม่ยาก
ข้อเสียของ Sigmoid Function
- ถ้า Input น้อยกว่า -5 หรือมากกว่า 5 ความชัน Slope จะเข้าใกล้ 0 จน Gradient หายไปหมด ทำให้โมเดล Train ไม่ไปไหน เรียกว่า Vanishing Gradient จะอธิบายต่อไป
- Output ไม่ Balance มี Mean ไม่เท่ากับ 0 เพราะมีแต่ค่าเป็นบวก ทำให้ Optimize ยาก
- ใช้แล้วโมเดลมักจะ Converge ช้า
ข้อเสียเหล่านี้ทำให้ปัจจุบัน Sigmoid Function เสื่อมความนิยมลงไป ถูกแทนที่ด้วย ReLU Function ที่เราจะอธิบายต่อไป
Train Neural Network
Deep Neural Network with 2 Hidden Layers using Sigmoid
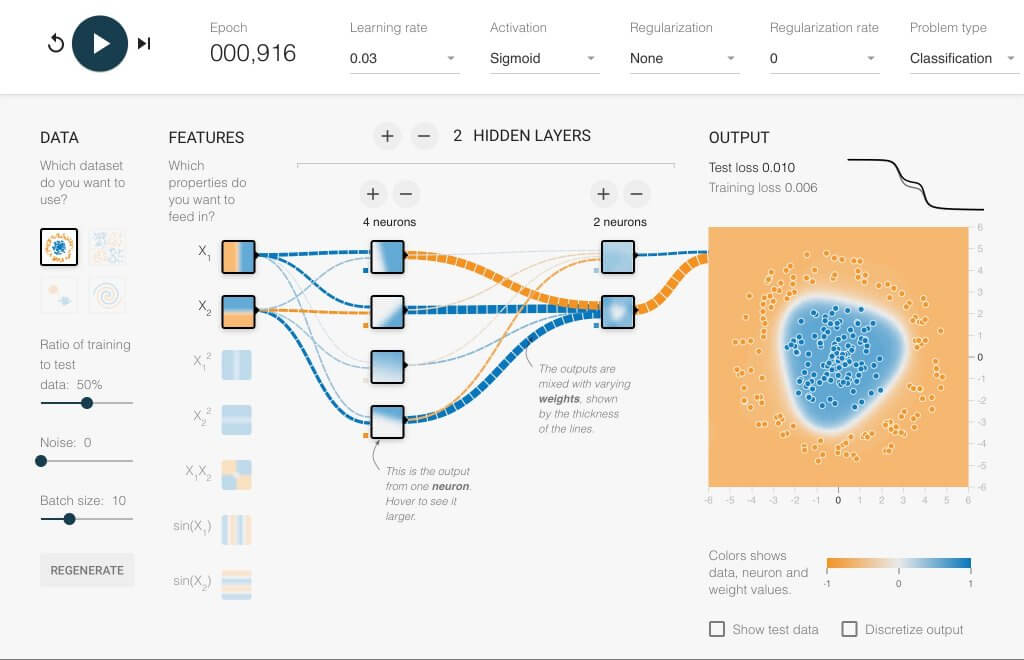
สังเกตว่าต้องเทรนมากถึง 1,000 Epoch ถึงจะ Converge และช่วงแรก Training Loss และ Test Loss ไม่ลดเลย
หมายเหตุ
จริง ๆ แล้วระบบประสาท นิวรอนในสมองมีหลายชนิด และทำงานซับซ้อนกว่านี้มาก ปัจจุบันจึงไม่ค่อยนิยมเปรียบกับการทำงานของสมองแล้ว
Credit
- http://cs231n.github.io/neural-networks-1/
- https://towardsdatascience.com/activation-functions-neural-networks-1cbd9f8d91d6
- https://en.wikipedia.org/wiki/Activation_function
- https://playground.tensorflow.org