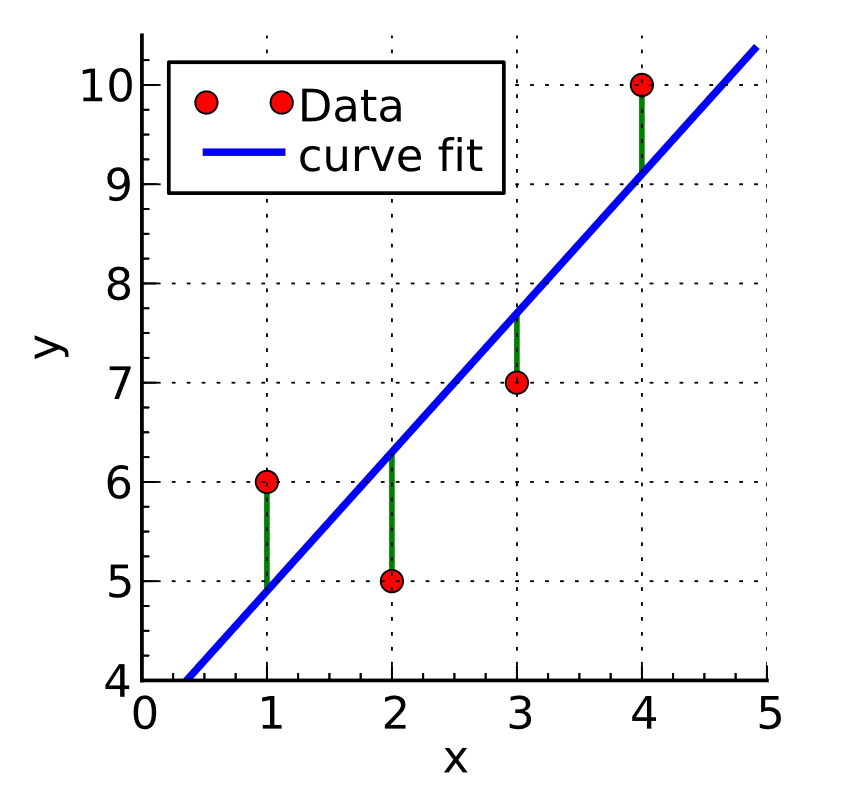
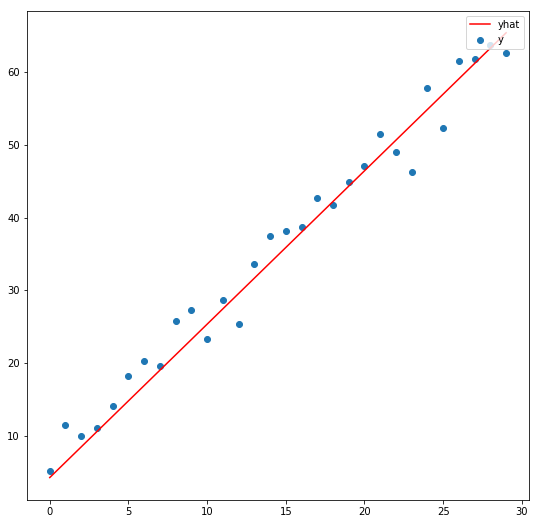
จาก ep ที่แล้วที่เราเล่าถึงคอนเซ็ปต์ของ SGD ไป ใน ep นี้เราจะมาดูตัวอย่างโค้ดแบบง่ายที่สุด ซับซ้อนน้อยที่สุด ซึ่งเป็นพื้นฐานสำคัญของ Machine Learning แบบ Neural Network คือ Linear Regression ด้วยอัลกอริทึม Stochastic Gradient Descent (SGD)

แต่ในการหา Slope นั้นเราไม่ต้อง Diff เอง แต่เราจะใช้ความสามารถ ของ Pytorch เรียกว่า Autograd หา Gredient ของ Parameter ทุกตัวให้โดยอัตโนมัติ

โมเดลที่เราใช้ครั้งนี้จะเป็น Linear Equation แบบง่าย ๆ ไม่มี Deep Learning หลายชั้น มี Parameter แค่ 2 ตัวเท่านั้น คือ Slop และ จุดตัดแกน y ไม่มี Activation Function ใด ๆ ทั้งสั้น

Loss Function ที่เราใช้ในเคสนี้คือ Mean Squared Error

Illustration of least squares fitting. The data (red dots) are at co-ordinates (1,6), (2,5), (3,7) and (4,10). A linear approximation is obtained using least-squares estimation (blue line). Credit: https://commons.wikimedia.org/wiki/File:Linear_least_squares_example2.svg
Illustration of least squares fitting. The data (red dots) are at co-ordinates (1,6), (2,5), (3,7) and (4,10). A linear approximation is obtained using least-squares estimation (blue line). Credit: https://commons.wikimedia.org/wiki/File:Linear_least_squares_example2.svg

เรามาเริ่มกันเลย

Open In Colab

แชร์ให้เพื่อน:

Share

บทความที่เกี่ยวข้อง:

  1. Gradient Descent คืออะไร อะไรคือ การเคลื่อนลงตามความชัน, Stochastic Gradient Descent (SGD) คืออะไร – Optimization ep.1
  2. Refactor สร้าง Optimizer สำหรับอัพเดท Parameter ของ Neural Network ในการเทรน Deep Learning – Neural Network ep.6
  3. lr_find หา Learning Rate ที่ดีที่สุดในการเทรน Machine Learning โมเดล Deep Neural Network ด้วย Callback – Neural Network ep.12
  4. สร้าง Training Loop แบบง่าย เริ่มต้นเทรน Neural Network ด้วย Mini-Batch SGD – Neural Network ep.4
Surapong Kanoktipsatharporn on FacebookSurapong Kanoktipsatharporn on LinkedinSurapong Kanoktipsatharporn on Rss
Surapong Kanoktipsatharporn
Solutions Architect at Bua Labs
The ultimate test of your knowledge is your capacity to convey it to another.

Published by Surapong Kanoktipsatharporn

The ultimate test of your knowledge is your capacity to convey it to another.