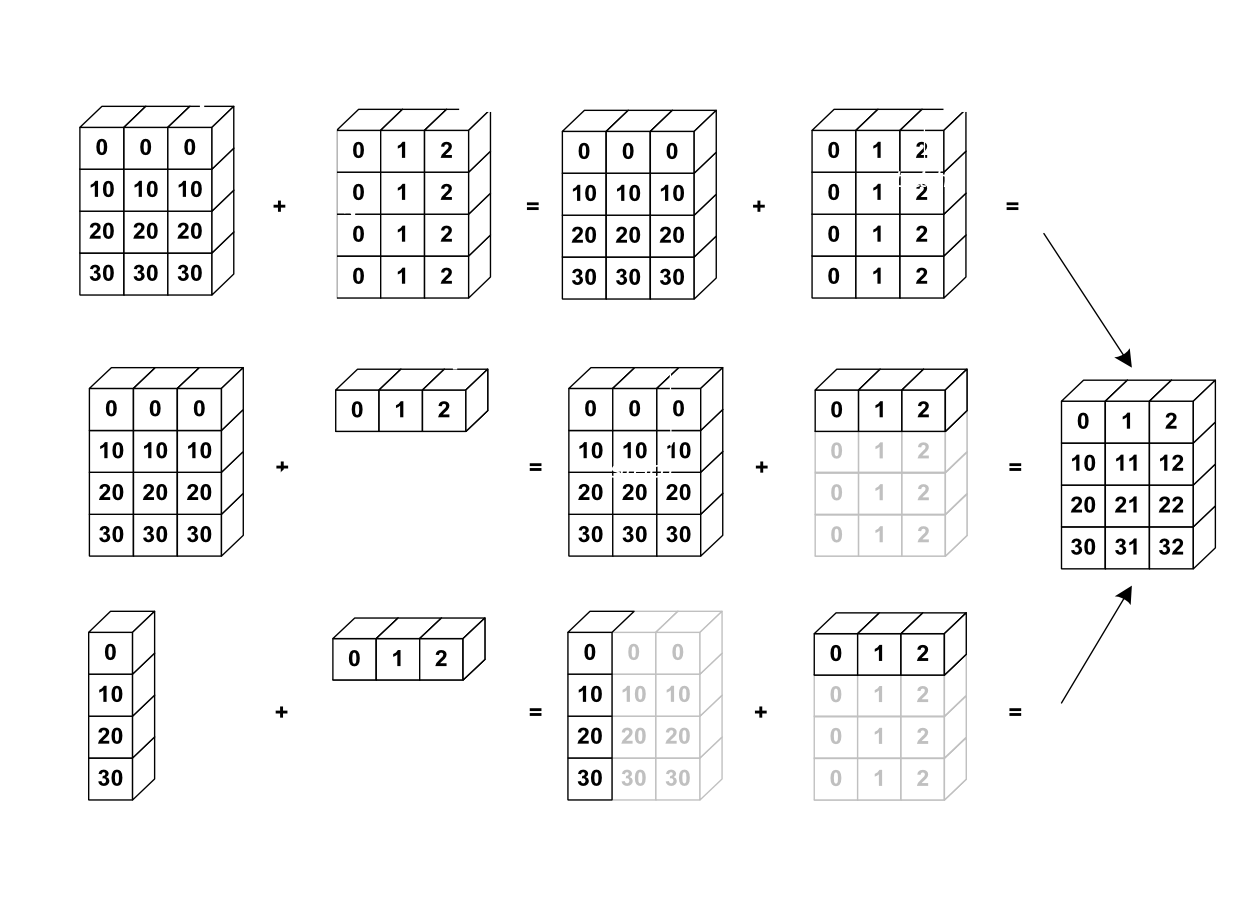
ในการเรียนรู้ Neural Network เราจะพบเจอโค้ดที่ใช้ List, Vector, NumPy Array ไปจนถึง High-Order Tensor หมายถึง Array ที่มีมากกว่า 2 มิติขึ้นไป เช่น 3 มิติ 4 มิติ หรือ 5 มิติ จนเป็นเรื่องธรรมดา ใน ep นี้เราจะมาเรียนรู้การใช้งาน Tensor ทำความเข้าใจ element-wise, broadcasting operations
Vector และ List คืออะไร
Vector (เวกเตอร์) และ List (ลิสต์) คือ ภาชนะบรรจุข้อมูลที่มีขนาดเท่ากัน ชนิดเดียวกัน ที่มี 1 มิติ เช่น [1, 2, 3, 4]
NumPy Array และ Matrix คืออะไร
NumPy Array (นัมไพ อาเรย์) และ Matrix (เมตริกซ์) คือ ภาชนะบรรจุข้อมูลที่มีขนาดเท่ากัน ชนิดเดียวกัน ที่มี 2 มิติ เช่น
[[1, 2, 3],
[4, 5, 6] ,
[7, 8, 9]]
Tensor คืออะไร
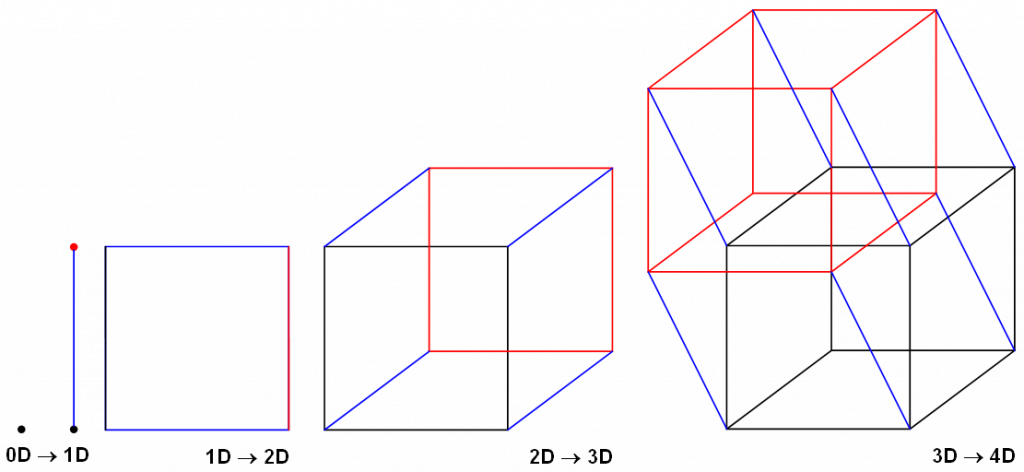
Tensor (เทนเซอร์) คือ ภาชนะบรรจุข้อมูลที่มีขนาดเท่ากัน ชนิดเดียวกัน ที่มีกี่มิติก็ได้ เช่น รูปสี ความละเอียด 224 x 224 Pixel จำนวน 10 รูป จะมีข้อมูล 4 มิติ ดังนี้ (10, 3, 224, 224) และสมมติเรามีข้อมูล 10 รูปแบบนี้ จาก 12 เดือน ก็จะเป็น 5 มิติ (12, 10, 3, 224, 224)
เราสามารถออกแบบมิติข้อมูลเพื่อใช้งานได้อย่างอิสระ
หมายเหตุ
- NumPy Array จริง ๆ คือ N-Dimension (ndarray) ก็สามารถใช้บรรจุข้อมูล กี่มิติก็ได้เช่นกัน แต่นิยมใช้ 1-2 มิติ
- 3 ในรูปสี คือ 3 Channels RGB
- การเรียงมิติไหนก่อนหลัง ขึ้นกับแต่ละ API
- Rank Number หมายถึง จำนวนมิติ ของ Tensor เช่น ตัวอย่างด้านบน (10, 3, 224, 224) จะเรียกว่า Rank 4 Tensor
ข้อดีของ Tensor เปรียบเทียบกับ NumPy Array
Tensor นั้นมีข้อดีหลายอย่างกว่า NumPy Array คือ สามารถใช้ GPU และรองรับ Autograd สามารถคำนวน Diff หา Gradient ให้อัตโนมัติ ทำให้เหมาะที่จะนำมาใช้สร้าง Deep Neural Network ในปัจจุบัน ที่เทรนโมเดลด้วยอัลกอริทึม Gradient Descent และ Backpropagation

และเมื่อมี GPU แทนที่เราจะเขียนโปรแกรม วน Loop ทำ Operations ทีละ Element เราจึงต้องปรับ Mindset ออกแบบด้วยแนวคิด Vectorization คือ ทำทุกอย่างให้เป็น Vector, Array หรือ Tensor แล้วทำ Operation นั้น ๆ พร้อม ๆ กันทีเดียวหมด ขนานกันไปเลย ด้วย GPU ซึ่งจะช่วยเพิ่มความเร็วขึ้นกว่าวน Loop ทำทีละอัน หลายร้อย หลายพันเท่า