ทำไมต้อง Vectorization เปรียบเทียบความเร็ว คูณเมตริกซ์ Matrix Multiplication (Dot Product) ด้วยอัลกอริทึม Vectorization และวน Loop – Tensor ep.3

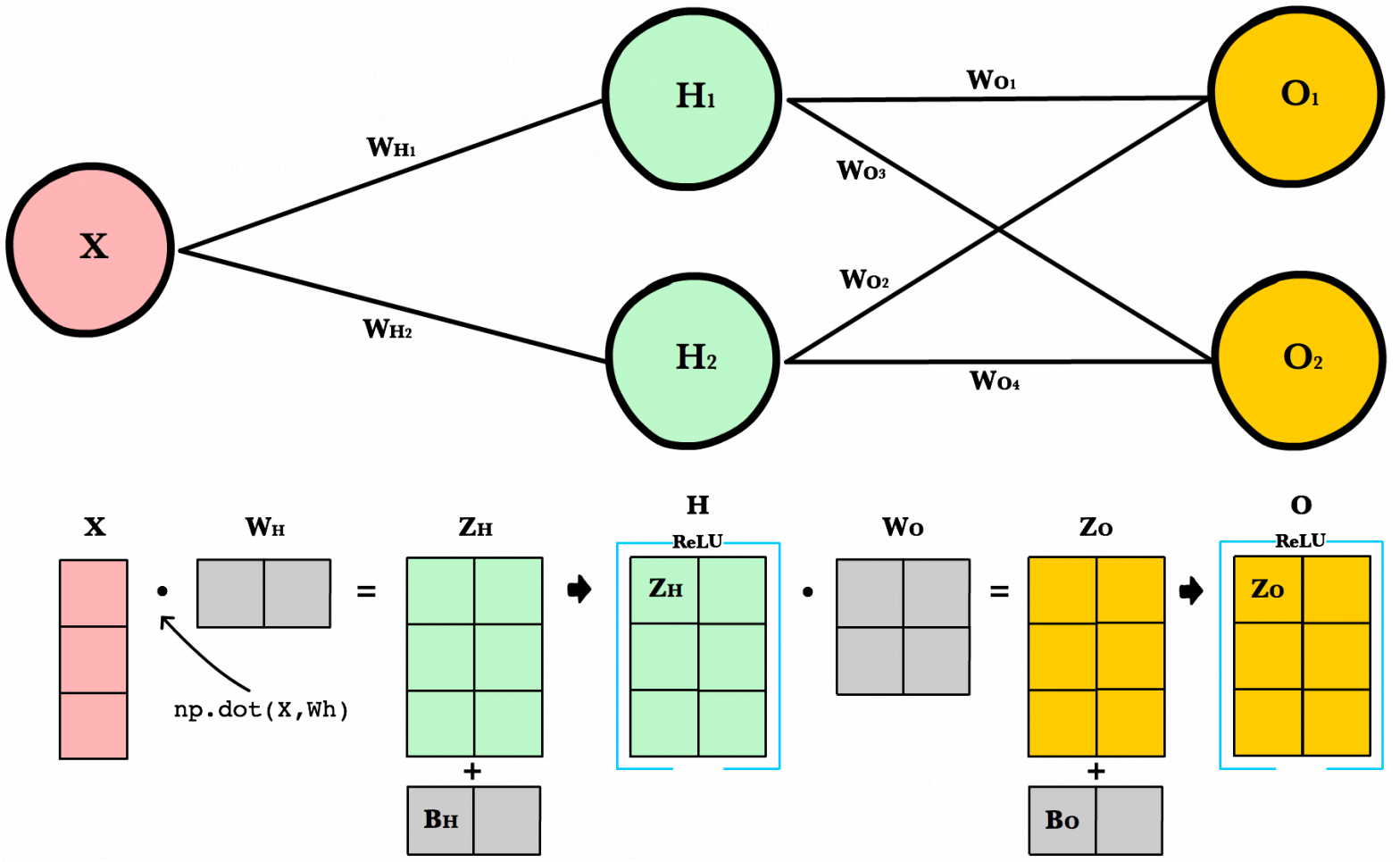
จาก ep ที่แล้ว ที่เราเรียนรู้ถึงคุณสมบัติพิเศษ ของ Tensor ที่จะมาช่วยในการคำนวนต่าง ๆ เมื่อเรามองเจาะลึกเข้าไปภายในของ Deep Neural Network เราจะพบว่าในขณะที่เราเทรน หรือขณะใช้งานโมเดลก็ตาม Mathematical Operations การดำเนินการทางคณิตศาสตร์ส่วนใหญ่ที่เกิดขึ้นก็คือ การคูณเมตริกซ์ โดยเฉพาะการคูณเมตริกซ์ (Matrix Multiplication) แบบ Dot Product

การคูณเมตริกซ์ที่รวดเร็วแม่นยำ มีผลต่อการทำงานของ Neural Network เป็นอย่างมาก

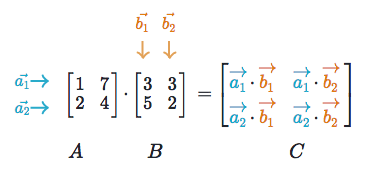
ดังนั้นใน ep นี้เราจะมาเรียนรู้การคูณเมตริกซ์ โดยใช้ คุณสมบัติพิเศษ ของ Tensor เช่น Element-wise, Broadcasting เพื่อให้เราออกแบบโมเดล และปรับปรุงอัลกอริทึม ให้เป็นแบบ Vectorization ให้โมเดลทำงานแบบขนาน บน GPU ได้ มีประสิทธิภาพดีขึ้น ตามที่เราต้องการ

เรามาเริ่มกันเลย

Keng Surapong

Project Manager at Bua Labs

The ultimate test of your knowledge is your capacity to convey it to another.